Wie bewertet Skitourenguru das Lawinenrisiko?

1. Einleitung

Seit dem Winter 2024/25 basiert Skitourenguru auf einer neuen Methode, einer Variante von SLABS (Screening the Likelihood of Avalanches on Backcountry Ski tours). Skitourenguru sieht sich in der Pflicht für Transparenz zu sorgen. Die technischen Details der Methode wurden deshalb in einer begutachteten Open-Access-Publikation veröffentlicht:

Degraeuwe at al. (2024): Screening the Likelihood of Avalanches on Backcountry Ski tours (SLABS) - An improved probabilistic method to assess the avalanche risk on backcountry ski tours.

Das Paper beschreibt ein Modell namens SLABS. Dieses wurde von Unfalldaten und Nicht-Unfalldaten trainiert. Diese News fasst die wichtigsten Neuerungen von SLABS zusammen. Da Skitourenguru ausschliesslich mit White-Box-Methoden arbeitet, sind die Innereien des Modells bekannt. Genau genommen werden während der Entwicklung viele Modelle berechnet und dann miteinander verglichen. Zum Einsatz kommt schliesslich ein Modell mit den Namen SLABS-1LR.

Der Zusatz 1LR steht für die sogenannte Einstufenregel (1-Level-Rule). Diese Regel besagt, dass ausserhalb der im Lawinenlagebericht genannten Expositionen und Höhenlagen eine Gefahrenstufe tiefer angenommen wird. Die Einstufenregel konnte von Winkler et al (2021) in der ungefähren Grössenordnung bestätigt werden. Schon jenes Paper zeigt aber auch, dass der absoluten Höhe eine viel wichtigere Rolle zukommt, als bisher angenommen. Um diesen Befund korrekt abzubilden, nimmt SLABS-1LR zusätzlich zur Einstufenregel auch die Höhe ele in das Modell auf.

Dass der Einstufenregel ein zweites Leben eingehaucht wird, hat einen guten Grund: Diese Regel ist Garant dafür, dass in allen Fällen das resultierende Lawinenrisiko ansteigt, wenn die Gefahrenstufe steigt. Die Modellgüte nimmt durch den Rückgriff auf die Einstufenregel zwar geringfügig ab, aber das Modell ist nur marginal schlechter als das originale Modell SLABS. Sowohl SLABS, wie auch SLABS-1LR sind besser als die bis anhin verwendete QRM.

2. Segment-Risiko

Die unten stehende Formel zeigt, wie aus einer Reihe von Eingangsgrössen (z.B. maximale Neigung im Hang, Gefahrenstufe, Höhe) die Unfallwahrscheinlichkeit für ein 10m-Segment berechnet werden kann:

Eingangsgrössen:

• rdl: Gefahrenstufe im Bereich [1..4]. Zwischenstufen werden verarbeitet, sofern sie vorhanden sind.
• msa70: Die Neigung an der steilsten Stelle im zugeordneten Relevanten Hangbereich. Jedem Punkt in den Alpen wird ein sogenannter Relevanter Hangbereich zugeordnet. Die steilste Stelle auf diesem Hang ist massgebend für den fraglichen Punkt. Der Zusatz 70 steht für einen Kontrollradius in Metern, der die grundsätzliche Grösse des Relevanten Hangbereiches steuert. Die tatsächliche Grösse des Relevanten Hangbereiches verändert sich aber je nach Beschaffenheit des Geländes (v.a. in Abhängigkeit von Neigung und Planarkurvatur).
• ele: Absolute Höhe des Ortes.
• dce: Relative Höhe gegenüber der im Lawinenbulletin genannten kritischen Höhe. Angenommen das Lawinenbulletin warne vor Hängen oberhalb 2000m und wir befinden uns auf 2350m, dann wird dce=+350m. dce kann auch negativ sein. Die Logik wird umgedreht, wenn das Lawinenbulletin vor Höhen bspw. unterhalb 1800m warnt: Angenommen wir befinden uns auf 1950m, dann wird mit dce=-150m gerechnet. Schliesslich befinden wir uns dann ausserhalb der Höhenstufen vor denen das Lawinenbulletin warnt.
• aof: Hier geht es um die Frage, ob unser Hang Expositionen aufweist, vor denen das aktuelle Lawinenbulletin warnt. Da ein konkreter Hang immer viele Expositionen aufweist, wird berechnet welcher Anteil der Hangexpositionen in den sogenannten kritischen Expositionen liegt. aof ist deshalb eine Zahl im Bereich [0..1]. Wenn alle unsere Hangexpositionen ausserhalb der kritischen Expositionen liegen, dann gilt aof=0. Wenn alle unsere Hangexpositionen innerhalb der der kritischen Expositionen liegen, dann gilt aof=1.

Aus diesen Eingangsgrössen lässt sich eine Wahrscheinlichkeit einer Lawinenauslösung für ein 10m-Segment berechnen. Genau genommen sprechen wir von einer Lawinenauslösung dessen Konsequenzen dermassen gravierend sind, dass mutmasslich eine Meldung an das SLF erfolgt, sodass das entsprechende Ereignis Eingang findet in die Schadensdatenbank des SLF (SLDB).

Man beachte, der genaue Zusammenhang zwischen den Eingangsgrössen und der Ausgangsgrösse ist nicht-linear. Das heisst das Lawinenrisiko steigt über-proportional, wenn eine Eingangsgrösse steigt:

• Je höher die Gefahrenstufe, desto grösser das Lawinenrisiko. Das Lawinenrisiko steigt von Gefahrenstufe zu Gefahrenstufe um den Faktor 4.3.
• Je steiler die "steilste Stelle im Hang", desto grösser das Lawinenrisiko. Bei einem 5°-Sprung steigt das Lawinenrisiko ca. um einen Faktor 3 bis 5. genaue Zahlen finden sich in Tabelle 1 des erwähnten Papers.
• Je höher der Ort, desto grösser das Lawinenrisiko.
• Je tiefer der Punkt in der Kernzone (kritische Expositionen, kritische Höhenlage gemäss Lawinenbulletin) liegt, desto grösser das Lawinenrisiko.

Ganz offensichtlich wird nebenbei mit SLABS der Nachweis erbracht, dass sich ein Anstieg der Gefahrenstufe von 2-Mässig auf 3-Erheblich durch einen Verzicht auf 5° Neigung in etwa kompensieren lässt. Mehr zu diesem Thema findest du im Artikel Reduktionsmethoden sind falsch???.

Die Formel enthält auch eine Reihe von Konstanten (schwarz), sowie eine nicht-lineare Funktion (fs). Ein tieferes Verständnis der Formel geht nicht ohne Kenntnisse moderner Regressionsanalyse. Konkret kommt ein GAM (Generalized Additive Model) mit einem LOGIT-Link zum Einsatz. Der inverse LOGIT sorgt für den starken exponentiellen Anstieg des Lawinenrisikos mit den Eingangsgrössen.

Doch wie wird mit Punkten umgegangen, die sich im Einzugsbereich von Warnregionen mit unterschiedlicher Gefahrenstufe befinden? Ein konkreter Punkt im Gelände kann nur dann eindeutig einer Warnregion zugeordnet werden, wenn er sich in einer 20%-Zentrumszone der Warnregion befindet. Um die Zentrumszone zu bestimmen wird für jede Warnregion ein maximaler Kreis mit dem Radius r bestimmt der gerade noch Platz findet in der Warnregion. Wenn sich ein Punkt mindestens 0.8*r vom Warnregionsrand entfernt befindet, dann wird angenommen er liege im Zentrum. Meistens befindet sich ein Punkt jedoch im Einzugsbereich von mehreren Warnregionen. Skitourenguru berechnet die Lawinenrisiken für alle Warnregionen im Einzugsbereiches des fraglichen Punktes. Anschliessend wird ein gewichtetes geometrisches Mittel der Lawinenrisiken bestimmt. Die Gewichte hängen von der Distanz zu den fraglichen Warnregionen ab. Durch diese Prozedur werden Sprünge an Warnregionsgrenzen verhindert.

Das Paper zu SLABS zeigt nicht nur auf welche Eingangsgrössen wichtig sind, es zeigt auch welche Grössen keinen relevanten Einfluss auf das Lawinenrisiko haben (siehe Kapitel 5.2 im Paper):

• Lawinenproblem: So wird bspw. offenkundig, dass die Ursache der Lawine (Lawinenproblem) keinen Einfluss auf die Grösse des Lawinenrisikos hat. Dies hängt damit zusammen, dass das Lawinenproblem nicht Träger von quantitativer Information ist. Dieser Befund deckt sich mit den Bemühungen der Lawinenwarner:innen die Grösse der Gefahr ausschliesslich in die Gefahrenstufe einfliessen zu lassen. Ein Altschnee-3er soll grundsätzlich keine grössere Gefahr aufweisen, als ein Triebschnee-3er. Diese Einschränkung stellt in keinster Weise den Nutzen des Lawinenproblems in Frage. Beim Lawinenproblem geht es aber um die Frage nach dem was und nicht primär um die Frage wie viel.
• Walddichte: Die Walddichte kann keinen wesentlichen Beitrag zum Modell leisten. Dies hängt mit zwei Gründen zusammen. Einerseits wird "Bewaldung" bereits bei der Bestimmung des relevanten Hangbereiches berücksichtigt. Anderseits ist die Walddichte stark korreliert mit der Höhe.
• Geländekurvaturen: Die Kurvatur kann keinen wesentlichen Beitrag zum Modell leisten. Die Planarkurvatur wird bereits berücksichtigt bei der Bestimmung des relevanten Hangbereiches.
• Kammnähe: Auch die Kammnähe kann keinen wesentlichen Betrag zum Modell leisten. Dies hängt mit der starken Korrelation (0.66) zur Höhe zusammen.
• Absturzgeschwindigkeit: Auch Grössen, die im Zusammenhang mit den Konsequenzen einer Lawinenauslösung stehen können keinen Beitrag zum Modell leisten. Alle Grössen, die mit den Konsequenzen verbunden sind (z.B. Absturzgeschwindigkeit, Verschüttungstiefe) weisen eine hohe Korrelation mit dem Höhenmodell auf. Das Höhenmodell ist kein Perpetuum-Mobile, das beliebig viel Information produzieren kann. Bereits durch die Aufnahme von ele und msa70 ist ein guter Teil derjenigen Information abgedeckt, die das Höhenmodell zu bieten hat. Modelle, die auf vielen Eigenschaften basieren, die direkt aus dem Höhenmodell gewonnen wurden, sind kritisch zu begutachten.

Die Unfallwahrscheinlichkeit für ein 10m-Segment gibt uns bereits die Möglichkeit einen Routenverlauf grün, orange oder rot einzufärben. Dazu sind jedoch Schwellwerte notwendig. Diese werden folgendermassen angesetzt:

• Schwellwert grün-orange: Bleibt das Publikum auf grünen Segmenten, können 80% der Unfälle vermieden werden.
• Schwellwert orange-rot: Meidet das Publikum rote Segmente, können 60% der Unfälle vermieden werden.

Mhr Information zu diesen Schwellwerten findet du im erwähnten Paper.

3. Routen-Risiko

Nun kennen wir die Auslösewahrscheinlichkeit für ein 10 m Segment. Diese Auslösewahrscheinlichkeit bezieht sich auf ein Ereignis das Eingang findet in die Schadensdatenbank des SLF. Multiplizieren wir diese Auslösewahrscheinlichkeit mit einem weiteren Faktor Fx, dann erhalten wir die Auslösewahrscheinlichkeit für einen tödlichen Unfall. Das Produkt der Faktoren Fx und Fra10m kann mit Hilfe eines Durchschnitts-Szenarium bestimmt werden. Gemäss Winkler (2017) ist bekannt, dass auf ca. 114'000 Personentage ein Todesoper fällt. Die durchschnittliche Länge einer Skitour liegt bei 5050 m. Mit Hilfe dieser Angaben ist es möglich das Produkt der Faktoren F=Fx*Fra10m zu bestimmen.

Dadurch kennen wir die Sterbenswahrscheinlichkeit für jedes 10m-Segment, sofern ein Lawinenbulletin und ein Höhenmodell zur Verfügung steht. Wahrscheinlichkeiten können bei stochastischer Unabhängigkeit kombiniert werden, indem Gegenwahrscheinlichkeiten aufmultipliziert werden. Im Falle einer Skitour ist stochastische Unabhängigkeit jedoch nicht gegeben. Ein Beispiel: Wir traversieren einen 50 m breiten Hang. Die Sterbenswahrscheinlichkeit sei gleich auf allen fünf 10 m langen Segmenten. Wenn wir bereits drei Segmente ohne eine Lawinenauslösung durchquert haben, dann sinkt die Sterbenswahrscheinlichkeit für die letzten zwei Segmente. In einem gewissen Sinne machen wir uns das Wissen um drei negative (negativ im Sinne von nichts ausgelöst) indirekten Stabilitätstests zu nutze. Um diesem Umstand Rechnung zu tragen, wird folgendermassen gerechnet:

Eine Skitour wird in 100 m lange Abschnitte unterteilt. Jeder dieser Abschnitte besteht aus 10 Segmenten der Länge 10 m. Zunächst wird das Maximum der Sterbenswahrscheinlichkeit für jeden 100m-Abschnitt berechnet. Anschliessend werden für die resultierenden Sterbenswahrscheinlichkeiten die sogenannten Gegenwahrscheinlichkeiten aufmultipliziert. So erhalten wir eine Sterbenswahrscheinlichkeit für die einmalige Begehung/Befahrung der Route.

Eine Skitour wird jedoch doppelt begangen/befahren: Ein mal im Aufstieg, ein mal in der Abfahrt. Auch hier stellt sich die Frage nach der stochastischen Unabhängigkeit. Hier gibt es zwei widerstreitende Effekte:

1. Wenn während des Aufstiegs keine Lawine ausgelöst wurde, sinkt - im Durchschnitt - die Wahrscheinlichkeit bei der Abfahrt eine Lawine auszulösen. Die Hänge der Route haben schliesslich während dem Aufstieg einen Stabilitätstest bestanden. Dies gilt natürlich nur, wenn in der Nähe der Aufstiegsspur abgefahren wird. Eine Arbeit von Grimsdottir and McClung (2006) zeigt sehr eindrücklich auf, dass die erste Person, die einen Hang befährt das höchste Risiko trägt. Den anderen die Vorfahrt zu lassen ist im Falle vom Skisport also keine Geste der Höflichkeit.
2. Auch wenn in der Nähe der Aufstiegsspur abgefahren wird, wird im Schnitt mehr Gelände angeschnitten und steileres Gelände betreten. Es hat seinen guten Grund, dass ca. 59% der Unfälle bei der Abfahrt stattfinden (Techel and Zweifel, 2013).

Welcher der beiden Effekte überwiegt, hängt von den aktuellen Verhältnissen, von der Befahrungshistorie und von der Spur im Auf- und Abstieg ab. Wir gehen davon aus, dass sich diese zwei Effekte in etwa kompensieren. Wir gehen also von stochastische Unabhängigkeit für die zwei Ereignisse "Aufstieg" und "Abfahrt" aus. Wir erhalten die Sterbenswahrscheinlichkeit für die doppelte Begehung/Befahrung indem wir die Sterbensgegenwahrscheinlichkeiten quadrieren und von 1 abziehen. Damit steht uns die Sterbenswahrscheinlichkeit für unsere Skitour zur Verfügung. Man beachte es handelt sich bei dieser Methode um einen Schätzer. Sterbenswahrscheinlichkeiten für eine Skitour variieren von 1:100 (rot) und 1:10'000'000 (grün). Ich Schnitt liegt sie bei 1:100'000. Die Angaben sind beziehen sich immer auf "Anzahl Personentage".

4. Risiko-Indikator

Skitourenguru könnte für jede Skitour die Sterbenswahrscheinlichkeit anzeigen. Dies macht aus zwei Gründen wenig Sinn:

1. Es handelt sich um einen Schätzer basierend auf dem Lawinenbulletin und dem Gelände. Die reale Sterbenswahrscheinlichkeit kann erheblich von diesem Schätzer abweichen.
2. Solche Wahrscheinlichkeiten sagen uns nichts. Sind wir bereit auf eine Skitour einzusteigen, die eine Sterbenswahrscheinlichkeit von 1:25'876 aufweist? Der Homo-Sapiens hat keinen Sinn für Proportionen auf einer exponentiellen Skala.

Die Risiko-Akzeptanz hängt stark vom gesellschaftlichen Kontext ab. So findet bspw. das Eingehen eines Risikos eher Akzeptanz wenn ein hoher Prestigegewinn (z.B. viel Geld) dadurch einhergeht. Alltägliche Risiken (z.B. Verkehr) finden eher Akzeptanz, als selten eintreffende Ereignisse (z.B. Haifisch frisst Mensch). Menschliches Versagen wird im Allgemeinen eher akzeptiert, als ein technisches Versagen. Ein technisches Versagen gilt im Gegensatz zum menschlichen Versagen als vermeidbar. Die Wahrnehmung von Risiko ist vielerlei Verzerrungen (Bias) unterworfen. Die Bücher von Rolf Dobelli geben eindrückliche Beispiele von irrationaler Risiko-Wahrnehmung und irrationalem Risiko-Verhalten des Homo-Sapiens. Besser würden wir vom Homo-Errare sprechen.

Es kann deshalb aus prinzipiellen Gründen keine objektive Methode geben, um Sterbenswahrscheinlichkeiten als akzeptabel (eher grün) oder inakzeptabel (eher rot) zu klassifizieren. Der einzig gangbare Weg liegt in einer Befragung von Wintersporttreibenden, die diesen Sport ausüben. Aus diesem Grund hat Skitourenguru zwei Befragungen durchgeführt. Die Teilnehmenden mussten für 30 Touren bei 3 Lawinenbulletins Risiko-Indikatoren im Bereich [1..3] bestimmen:

• Erste Umfrage: Diese Umfrage ist abgeschlossen.
• Zweite Umfrage: Diese Umfrage läuft noch. Eine Teilnahme ist erwünscht!

Die folgende Grafik zeigt 180 Punkte (2*30*3=180). Jeder Punkt steht für eine Skitour bei einem konkreten Lawinenbulletin. Die x-Achse gibt die inverse Sterbenswahrscheinlichkeit auf einer logarithmischen Skala (Log10) an. Je kleiner der Wert, desto höher die Sterbenswahrscheinlichkeit. Die y-Achse gibt den durchschnittlichen Risiko-Indikator im Bereich von [0..3] aus der Umfrage wieder. Man beachte bei jeder Umfrage haben über 30 Personen mitgemacht. Je nach Ausbildungsniveau wurde die betreffende "Meinung" unterschiedlich gewichtet. Es zeigt sich jedoch, dass die geschätzten Risiko-Indikatoren gut konvergieren. Das heisst es gab eine relativ grosse Übereinstimmung. Mehr Information zu diesem Thema findet sich in der Auswertung der ersten Umfrage.

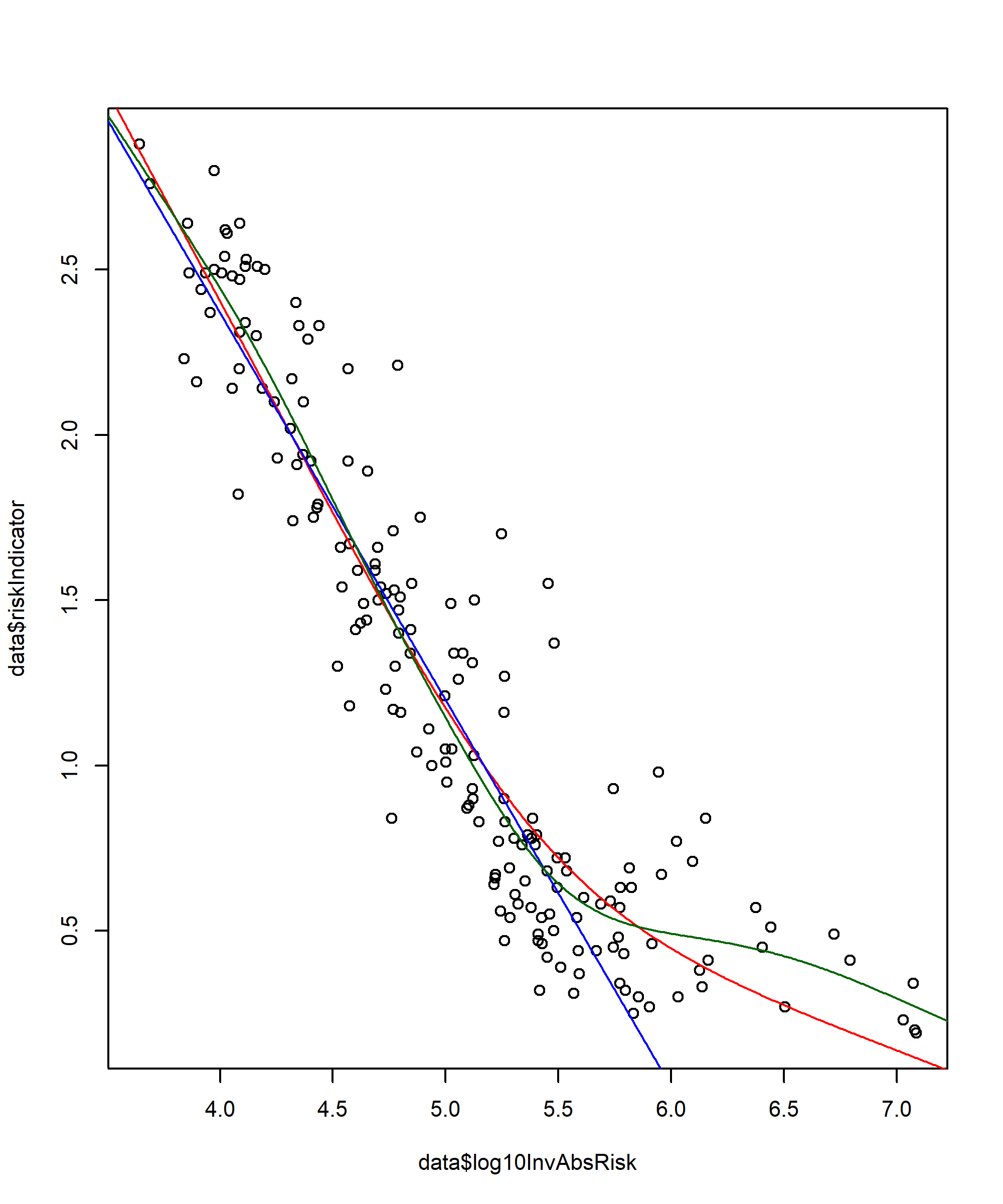
Bereits von Auge lässt sich ein klarer Zusammenhang zwischen der Sterbenswahrscheinlichkeit (x-Achse) und dem Risiko-Indikator (y-Achse) erkennen. Dieser ist übrigens annähernd linear. Es ist nun möglich ein GAM (Generalized Additive Model) einzupassen. Die rote Linie entspricht derjenigen Funktion, die eine Sterbenswahrscheinlichkeit in einen Risiko-Indikator umrechnen kann. Die leichte Nicht-Linearität des GAM wird nur im Bereich von Risiko-Indikator<0.5 (tief grüne Routen) wirksam.

Mittlerweile kennen wir als den Risiko-Indikator. Dieser ist in drei Klassen eingeteilt:

1. Grün: tiefes Risiko - Werte im Bereich [0..1]
2. Orange: erhöhtes Risiko - Werte im Bereich [1..2]
3. Rot: hohes Risiko - Werte im Bereich [2..3]

Der Risiko-Indikator sagt uns also etwas über die Sterbenswahrscheinlichkeit. Letztendlich geht es aber primär um die Klasse (grün, orange, rot). Die Zahl gibt uns aber einen guten Hinweis, ob wir nahe an einem Klassenwechsel sind. So mag eine Route mit einem Risiko-Indikator von 0.99 zwar noch grün sein, aber dessen Sterbenswahrscheinlichkeit ist fast identisch zu einer orangen Route mit einem Risiko-Indikator von 1.01. Man achte also auf die Zahl. Liegt sie eher im unteren, mittleren oder oberen Bereich der jeweiligen Klasse?

5. Fragen und Antworten

Was ändert sich für mich als Benutzer:in durch den neuen Algorithmus?

Für die Benutzer:innen änderst sich nichts. Die Risiko-Indikatoren weisen durch die neue Methode (SLABS-1LR) zwar eine bessere Qualität auf, die grundsätzlichen Unsicherheiten bleiben aber weiterhin bestehen. Diese sind v.a. auf den hohen Generalisierungsgrad und die relative Unsicherheit des Lawinenbulletins zurückzuführen.

Wie steht es um den Faktor "viel befahren"?

Zweifelsohne kommt dem Faktor "viel befahren" ein zentraler Stellenwert zu. Leider stehen keine zeitnahen Daten zu den Begehungen/Befahrungen in den Hängen der Alpen zur Verfügung. Auch Plattformen wie Strava, Garmin oder Suunto erhalten nicht annähernd genug Feedback vom Publikum, um eine angemessene Befahrungs-Historie abzubilden. Wenn sich Apple und Google zusammenschliessen würden, dann gäbe es ev. Aussicht auf ein reales Abbild von den Begehungen/Befahrungen, die in den Bergen stattfinden. Bekanntlich weiss unser Smartphone mehr über uns, als wir selber. Skitourenguru hat über einen Verbindungsmann bei Google die Frage abklären lassen: Die Ängste vor dem Themenkomplex "Privatsphäre" sind dermassen gross, dass bei Google selbst für interne Projekte die Hürden beim Zugriff auf Lokalisierungsdaten sehr hoch sein sollen. Das Problem könnte man folgendermassen umschreiben: Lokalisierungsdaten lassen sich nicht wirklich anonymisieren, bzw. anonymisierte Daten lassen sich durch Kombination mit anderen Datenquellen leicht wieder aufbrechen. Beispiel: Ich bin eine Bank und sehe alle Auszahlungen an den Bankomaten. Nun kombiniere ich diesen Datensatz mit anonymisierten Lokalisierungsdaten und kann so den anonymisierten Lokalisierungsdaten eine Identität zuweisen. Dadurch sehe ich aber gleich auch alles, was meine Kunden sonst noch so treiben.

Es gäbe eine Alternative: Moderne Lawinenverschüttetensuchgeräte (LVS) kommunizieren über Bluetooth bereits heute mit dem Smartphone. Theoretisch wäre es denkbar, dass durch das Einschalten des LVS die Aufzeichnung eines GPX-Trekks auf dem Smartphone beginnt und beim Abstellen endet. Anschliessend könnte - Einverständnis vorausgesetzt - der GPS-Trekk automatisch auf einen Server hochgeladen werden. Damit genügend Daten zur zeitnahen Befahrungs-Historie zusammenkommen, müssten aber mind. 30-70% der Benutzer:innen an ein solches System angebunden sein. Das ist im besten Fall Zukunftsmusik.

Das betrübliche Fazit: Es ist ausgeschlossen, dass Skitourenguru in einem absehbaren Zeithorizont zeitnahe Daten zu Befahrungen/Begehungen in das Modell integrieren kann. Letztendlich gilt das aktuelle Modell für durchschnittliche Verspurtheit, was auch immer das bedeuten mag. Ist ein Hang gar nicht verspurt, kann er risikoreicher sein, als das Modell suggeriert. Wurde der Hang in naher Vergangenheit stark befahren, kann das Risiko weit unter dem Modell-Output liegen.

Hängt die Grösse des relevanten Hangbereiches von der Gefahrenstufe ab?

Traditionelle Reduktionsmethoden schlagen vor, dass die steilste Stelle in einem mehr oder weniger grossen Bereich gesucht werden soll. Bei der GRM wurde ursprünglich folgendes vorgeschlagen:

1. Gering: Neigung wird am Ort aufgenommen (sa).
2. Mässig: Steilste Neigung wird 10 m um den Ort herum gesucht (msa40).
3. Erheblich: Steilste Neigung wird im ganzen Hang gesucht (msa70).
4. Gross: Steilste Neigung wird im ganzen Hang inkl. Auslaufbereich gesucht (msa100).

Während der Modellbildung wurde eine weitere Eigenschaft erzeugt, nennen wir sie gefahrenstufen-abhängige steilste Neigung. Je nach Gefahrenstufe wurde die steilste Stelle in einem anderen "Suchbereich" um den fraglichen Punkt herum gesucht. In obiger Auflistung wird die benutzte Variable mit Klammern angegeben. Im Paper wird die gefahrenstufen-abhängige steilste Neigung mit SA_p. bezeichnet. Während der Modellbildung konnte gezeigt werden, dass diese Eigenschaft keinen nennenswerten Beitrag zur Verbesserung der Modellgüte leisten kann (siehe Kapitel 5.2 im Paper).

Selbst wenn sich diese Eigenschaft als wichtig herausgestellt hätte, wäre dessen Integration in das Modell problematisch. Diese Eigenschaft ist nämlich korreliert (verwandt) mit der Gefahrenstufe (rdl). Wenn Eigenschaften miteinander korreliert sind, dann können Modelle instabil werden, da nicht mehr klar ist auf welche der miteinander verwandten Eigenschaften sich das Modell abstützen soll. Je nach Tainings-Daten können so sehr unterschiedliche Modelle resultieren.

Grundsätzlich lösen Schneebrettlawinen immer nach denselben physikalischen Gesetzen aus. Dies gilt auch für Schneebrettlawinen, die in einem Hang mit "geringer Lawinengefahr" ausgelöst wurden. Es ist deshalb fraglich, ob der unterschiedliche "Suchbereich" wirklich sinnvoll ist.

Werden Spontanlawinen abgedeckt?

Skitourenguru umfasst mit guten Gründen kein Modell für Spontanlawinen. Spontanlawinen werden auch als natürliche Lawinen bezeichnet. Gemäss Techel and Schweizer (2017) werden 95% der Lawinen durch die Beteiligten selbst ausgelöst. Der Mensch ist also Ursache und nicht ein zufälliges Oper der Lawinenauslösung. Lawinenunfälle mit Spontanlawinen sind sehr seltene Ereignisse. Eine Spontanlawine hat seinen eigenen Fahrplan. Sie kann den "Anstand haben" loszubrechen bevor wir die Gefahrenstelle durchqueren oder nachdem wir sie durchquert haben. Dass sich genau im Moment der Auslösung per Zufall jemand in der Gefahrenzone aufhält kommt zwar immer wieder vor, ist aber sehr unwahrscheinlich. Spontanlawinen sind ein Thema ab 3-Erheblich. Die Gefahrenskala des SLF umschreibt diesen Sachverhalt folgendermassen:

• 3-Erheblich: Spontane Lawinen sind möglich
• 4-Gross: Spontane und oft auch sehr grosse Lawinen sind wahrscheinlich

Die Entwicklung von Modellen zu Spontanlawinen wäre grundsätzlich nicht unmöglich. Die Umrechnung auf die von Skitourenguru verwendete Skala (Risiko-Indikator) ist aber alles andere als trivial: Plötzlich hängt die Unfallwahrscheinlichkeit nämlich nicht nur von der "Länge des angeschnittenen Geländes", sondern auch von der "Aufenthaltsdauer" ab. Es ist zwar möglich mit Hilfe einer Lawinensimulations-Software (z.B. RAMMS - Your Rapid Mass Movement Solution) Auslaufbereiche abzuschätzen, eine Aussage darüber zu machen, ob eine spezifische Spontanlawine in einem spezifischen Hang losbricht, wäre mit schwierig zu begründenden Annahmen verbunden.

Im Bereich zwischen 3-Erheblich und 4-Gross werden die Risiko-Indikatoren der betroffenen Skitouren auf Grund des exponentiellen Charakters von SLABS-1LR in den allermeisten Fällen sowieso orange oder rot. Es sei daran erinnert, dass das Lawinenrisiko um den Faktor 3-5 von Gefahrenstufe zu Gefahrenstufe ansteigt! Wir können es auch so ausdrücken: Wenn wir uns in einer Gefahrenzone betreffend "Spontanlawinen" aufhalten, dann riskieren wir praktisch immer auch eine Lawine auszulösen. Es ist eine Stärke von SLABS-1LR solche Situationen zu erkennen. Um zusätzlich vor Spontanlawinen zu warnen, wird ein entsprechender Hinweis in grauer (bei 3-Erheblich) oder roter (bei 4-Gross) Farbe ausgegeben. Wer Situationen mit Spontanlawinen meiden möchte, der bleibe oberhalb 3-Erheblich zu Hause.

Fazit: Die Entwicklung eines Modells für Spontanlawinen steht durchaus auf der Pendenzenliste von Skitourenguru, muss aber anderen Bemühungen die Qualität der Resultate von Skitourenguru zu verbessern den Vortritt lassen. Skitourenguru fokussiert also aus guten Gründen auf ein Modell, das die Auslösewahrscheinlichkeit von durch Personen ausgelösten Lawinen im Fokus hat.

Funktioniert das Modell auch bei Gleitschnee?

Gleitschneelawinen gleiten auf glattem Untergrund (z.B. Grashänge oder glatte Felsenzonen) ab. Den Abgangszeitpunkt von Gleitschneelawinen vorherzusagen ist kaum möglich, obwohl sie sich meist durch Gleitschneerisse (sogenannte Fischmäuler) ankündigen. Künstliche oder durch Personen ausgelöste Lawinen sind sehr unwahrscheinlich. Gleitschneelawinen sind also fast ausschliesslich Spontanlawinen. Dass Gleitschneelawinen in den letzten Jahren in der Öffentlichkeit und eine grosse Aufmerksamkeit erfahren, gibt eher dessen Eindrücklichkeit, denn dessen Relevanz für den Wintersport wieder.

Fazit: Da Gleitschneelawinen Spontanlawinen sind, gilt dasselbe wie für Spontanlawinen (siehe vorhergegangene Antwort).

Funktioniert das Modell auch bei Nassschnee?

Dass das Lawinenproblem keinen Beitrag zur Verbesserung der Modellgüte leisten kann, wurde im Kapitel 2 beschrieben. Dies gilt namentlich auch für das Nassschneeproblem. Nasschneelawinen sind gemäss Techel and Schweizer (2017) verantwortlich für ca. 10% der Lawinenunfälle.

Ein Blick auf die Europäische Gefahrenskala zeigt, dass die Definition der Gefahrenstufe ohne den Hinweis auf das Lawinenproblem auskommt. Mit anderen Antworten, es gibt keinen Grund zur Annahme, dass sich bspw. ein Nassschnee-3er in seinem Gefahrenausmass grundsätzlich von einem Altschnee-3er unterscheidet. Natürlich gibt es gewichtige Unterschiede zw. einem Altschneeproblem und einem Nassschneeproblem, nicht aber in Bezug auf dessen Gefahrenausmass. Das Gefahrenausmass wird alleinig in der Gefahrenstufe wiedergegeben.

Der GPS-Datensatz hat einen Bias!?

Skitourenguru sammelt seit bald 10 Jahren GPS-Tracks real unternommener Skitouren. Diese stammen von den Benutzer:innen der Plattformen Skitourenguru, Camp2Camp und Gipfelbuch. Damit stellt sich die Frage, ob die gesammelten GPS-Tracks repräsentativ für die Grundgesamtheit sind. Um dieser Frage nachzugehen hat Skitourenguru bereits bei der Entwicklung der QRM einerseits die GPS-Tracks mit anderen Datensätzen verglichen und anderseits sogenannte Sub-Sampling-Tests durchgeführt. Die Resultate, zusammengetragen im Artikel Participation-Bias, behalten ihre Gültigkeit auch in Bezug auf SLABS.

Die moderne Regressionsanalyse geht die Fragestellung mit einer sogenannten Residual-Analysis an. Eigenschaften, die in das Modell einfliessen (rdl, msa70, ele, dce, aof) werden Variates genannt. Sogenannte Co-Variates sind weitere Eigenschaften, die aus unterschiedlichen Gründen nicht Eingang in das Modell gefunden haben. Mit Hilfe der Residual-Analysis ist es u.a. möglich den Nachweis zu erbringen, dass eine spezifische Co-Variate keinen Beitrag zur Modellgüte leisten kann.

Bei der Frage, ob der GPS-Datensatz repräsentativ ist, geht es vor allem um die Frage ob diejenigen User:innen, die solche Daten sammeln und abgeben ein spezifisches Profil aufweisen. Im Fokus steht die Frage, ob es sich um Personen handelt, die eher exotisch oder eher klassisch unterwegs sind.

1. Exotisch: Personen, die eher auf anspruchsvollen Touren in abgeschiedenen Gebieten unterwegs sind.
2. Klassisch: Personen, die eher auf moderaten Modetouren, die gut erschlossen sind, unterwegs sind.

Nun hat A. Eisenhut eine Wildniskarte entwickelt. Genau genommen handelt es sich um eine Karte die das Thema Abgeschiedenheit behandelt. Der technische Name für diese Eigenschaft lautet Isolation (iso), schliesslich geht es um die Frage wie isoliert ein Punkt im Gelände von der "Zivilisation" (letzte Strasse, letzter Weg, letztes Siedlungsgebiet) ist. Es ist möglich sich diese Karte auf der WebApp von Skitourenguru anzeigen zu lassen. Dazu wähle man eine finale Route, öffne den Layer-Switcher (unten links auf der Karte) und aktiviere die Karte zur Abgeschiedenheit.

Die folgende Grafik zeigt die Pearson-Residuals der Co-Variate iso. Auf der x-Achse erscheint iso. Kleine iso-Werte (links) bedeutet "sehr erschlossen", grosse iso-Werte (rechts) bedeutet "sehr abgeschieden". Auf der y-Achse wird der standardisierte Fehler (ObservedValues - ExpectedValues) in Abhängigkeit der Co-Variate iso aufgezeichnet.

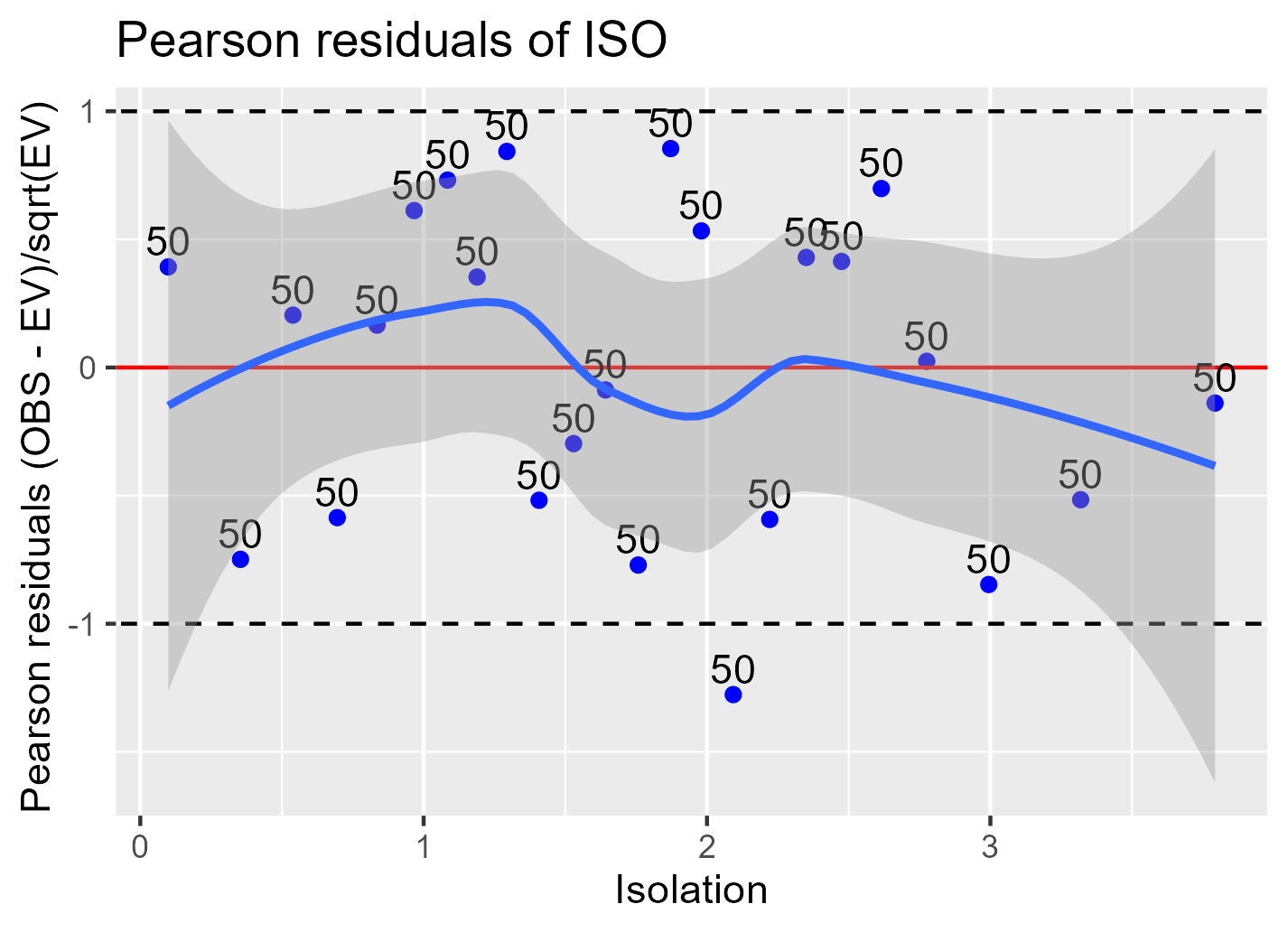
Wie aus der Grafik ersichtlich schwankt die blaue Kurve nahe am Nullpunkt. Vor allem ist aber kein deutlicher Trend in der Kurve ersichtlich. Die Co-Variate iso kann deshalb keinen Beitrag zur Modellgüte leisten. Es macht keinen Sinn sie in das Modell einfliessen zu lassen. Das Modell SLABS funktioniert also ähnlich gut unabhängig davon, ob wir in sehr abgeschiedenen Gebieten oder in sehr gut erschlossenen Gebieten unterwegs sind. Dem entsprechend ist es von untergeordneter Bedeutung, ob der Datensatz vor allem exotische oder klassische Touren enthält.

Fazit: Ob der GPS-Datensatz repräsentativ für die Grundgesamtheit ist, wissen wir nicht. Wir können aber zeigen, dass selbst wenn der Datensatz einseitig bezüglich dem Thema abgeschieden-erschlossen zusammengesetzt wäre, dieser Sachverhalt keinen grossen Einfluss auf die Ausgestaltung des Modells hätte.

Wie wird mit Fahrstrassen umgegangen?

Skitouren führen zu Beginn oft über Fahrstrassen. Meistens handelt es sich dabei um landwirtschaftlich oder forstwirtschaftlich genutzte Strassen, die typischerweise mit Schotter belegt sind und auf denen ein Fahrverbot gilt. Befinden sich solche Strassen in grosser Höhe und ausserhalb des Walds, bieten sie keinen Schutz. Liegt dort viel Schnee, sind sie oft sogar nicht mehr sichtbar. Wenn sie aber weiter unten liegen, dann ist es oft ausgeschlossen von einer Fahrstrasse aus einen weiter oben liegenden Hang auszulösen. Es besteht schlicht keine zusammenhängende Schneedecke zwischen dem Fahrbereich und dem Hang.

Um diesen Sachverhalt möglichst angemessen abzubilden schwächt Skitourenguru auf Fahrstrassen das Segment-Risiko um einen linear abfallenden Faktor ab:

1. Zwischen 0 m und 400 m: Unterhalb 400 m wird das Segment-Risiko um den Faktor 4 abgeschwächt. Das Risiko wird also durch 4 geteilt.
2. Zwischen 400 m und 1600 m: Zwischen 400 m und 1600 m sinkt der Faktor linear von 4 zu 1. D.h. auf sehr geringer Höhe wird das Risiko stark abgeschwächt, auf grösserer Höhe wird nur noch wenig abgeschwächt.
3. Zwischen 1600 m und 5000 m: Oberhalb 1600 m wird das Segment-Risiko nicht mehr abgeschwächt.

Man beachte letztendlich handelt Skitourenguru immer von Risiko-Relationen. Wird an einem Ort das Risiko abgeschwächt, bedeutet das implizit eine Erhöhung des Risikos an anderen Orten. Mit der Risiko-Abschwächung erreicht man so eine angemessene Risiko-Relation zwischen Orten auf einer betroffenen Fahrstrasse und allen anderen Orten.

Die Daten zu den Strassen stammen von OpenStreetMap (OSM). Ein Ort wird dann als eine Fahrstrasse klassifiziert, wenn er näher als 20 m von dieser entfernt liegt.

Was wenn eine Route durch einen Tunnel oder über einen Staudamm führt?

Manchmal führt eine Skitour durch einen Tunnel oder über einen Staudamm.

• Tunnel: Die auf den Tunnel projizierte Neigung kann sehr hoch sein, dennoch herrscht im Tunnel kein Lawinenrisiko. Skitourenguru setzt das Segment-Risiko in Tunnels deshalb auf null.
• Staudämme: Die talabwärts gelegene Flanke eines Staudamms ist in der Regel sehr steil bzw. vertikal oder sogar überhängend. Wird eine Route nicht exakt über den Dammbereich gelegt, kann dies zu roten Stellen (ein sogenannter "false Positive") führen. Skitourenguru setzt deshalb im Umkreis von 20 m um eine Staumauer herum das Segment-Risiko auf null.

Die notwendigen Daten stammen von OpenStreetMap (OSM).

Warum wird eine Skitour in Abschnitte ausgerechnet der Länge 100m eingeteilt?

Angenommen wir vergleichen die Neigungen von zwei Punkten im Gelände, können wir folgendes feststellen: Liegen sie nahe neben einander (z.B. in 10 m Distanz), dann ist der Unterschiede in der Neigung in der Regel sehr klein. Liegen sie weit auseinander (z.B. in 500 m Distanz), dann ist die Neigung an den Punkten unabhängig von einander. Auswertungen zeigen, dass die Ähnlichkeit zw. 50m und 200m stark sinkt. Liegt die Distanz höher als 100 m, sind die Neigungen nur noch lose miteinander verbunden.

Wie wird damit umgegangen, dass bei steilem Gelände im Zick-Zack aufgestiegen wird?

Skitouren werden in Form einer direkten Linie beschrieben. Diese gibt die Spitzkehren in steilem Gelände nicht wieder. Da es bei der Auslösung von Lawinen um die Länge des angeschnittenen Geländes geht, ist es wichtig die tatsächliche Routenlänge zu berücksichtigen: Bei einer Steilheit zwischen 18° und 45° wird davon ausgegangen, dass die Spur im Zick-Zack mit einer Neigung von 18° gelegt wird. Ab 45° ist es kaum mehr möglich mit Skiern aufzusteigen. Bei der Längenberechnung wird deshalb wieder auf die direkte Linie zurückgegriffen.